根据塞尔认知哲学的观点,语言智能是思维智能的基础,所以个人认为 NLP 在人工智能领域的重要性是要强于 CV 的。
已经学过的 NLP 的重要模型有循环神经网络(LSTM、GRU)等,但这些都是传统的基础模型,现阶段的 NLP 离不开 attention 机制,或者说离不开 Transformer. 因为 NLP 目前 SOTA(state-of-the-art) 的模型,如 BERT、GPT-3 等,都是基于 Transformer 的。
写在前面
根据塞尔认知哲学的观点,语言智能是思维智能的基础,所以个人认为 NLP 在人工智能领域的重要性是要强于 CV 的。
已经学过的 NLP 的重要模型有循环神经网络(LSTM、GRU)等,但这些都是传统的基础模型,现阶段的 NLP 离不开 attention 机制,或者说离不开 Transformer. 因为 NLP 目前 SOTA(state-of-the-art) 的模型,如 BERT、GPT-3 等,都是基于 Transformer 的。
因此,这里重点介绍 Transformer —— 一种自注意力机制的序列到序列模型。
要介绍 Transformer, 就需要介绍它的基础——attention (注意力机制),因为提出 Transformer 的那篇论文叫做《Attention is All You Need》,真的是非常的嚣张啊!
然后,我们从序列到序列模型(Seq2Seq)出发, 引出 Transformer 的介绍。
Attention 机制
为什么提出 attention ?
由于算力限制,不可能同时处理全部的信息,就像人不可能同时注意到环境中的全部信息一样,因此要有权重的对信息进行选择。
与卷积不同,注意力(attention)是对人类聚焦式注意力的建模,而卷积是对人类显著式注意力的建模。
显著式注意力:不依赖于任务,例如在一片白色中出现一个黑点,人们会自然而然地注意到这个黑点
聚焦式注意力:依赖于任务,例如在做阅读理解题目时候,我们更关注和题目相关的内容
attention 是怎么运算的?
- 注意力分布计算:用来计算对什么信息(数据)给予多少注意力(权重),即注意力的分布函数。
设:输入向量 $x=[x_1,…,x_N]$,查询向量 $q$ (根据任务给定,可以是动态生成的,也可以是 trainable 的)
注意力分布 (对第 $i$ 个输入给予的权重(即比例),权重和为 1) $\alpha_i=softmax(s(x_i,q))=\frac{exp(s(x_i,q))}{\sum_{j=1}^{N}{exp(s_j,q)}}$
其中,$s(·,·)$ 为打分函数,用来表示输入向量和查询向量的匹配度,它有四种形式,从中选择一种:加性模型、点积模型、缩放点积模型、双线性模型。
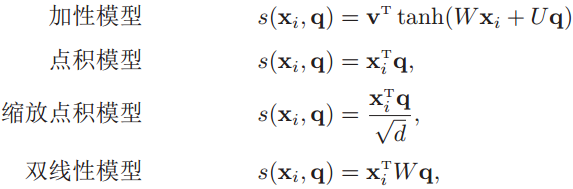
- 根据注意力分布计算经过注意力分配后的输入(聚合信息)
有五种计算方式:
比较简单的两种:
- 软性注意力: $att(x,q)=\sum_{i=1}^N{\alpha_ix_i}$ (加权平均)
- 硬性注意力: $att(x,q)=x_j\ \ where\ j=argmax_{i=1}^N{\alpha_i}$ (最大采样)或者在注意力分布式上进行随机采样(即根据$x_i$的概率$\alpha_i$采样)
重点是键值对注意力和多头注意力:
键值对 (K,V) 的键 K 用来计算 $\alpha_i$, 值 V 用来计算聚合信息,也就是说, 软/硬性注意力是根据输入 $x$ 计算对输入 $x$ 应该赋予的注意力分布,而键值对注意力是根据键 K 计算对值 V 应该赋予的注意力分布
- 键值对注意力:$att((K,V),q)=\sum_{i=1}^N{\frac{exp(s(k_i,q))}{\sum_j{exp(s(k_j,q))}}v_i}$
多头注意力的头是指查询向量,多个查询向量分别表示不同的任务,用$Q=[q_1,…,q_M]$表示,每个查询向量关注输入信息的不同部分
- 多头注意力:$att((K,V),Q)=att((K,V),q_1)\oplus…\oplus att((K,V),q_M)$
$\oplus\ is\ concat\ operation$
以上的注意力都是没有结构,实际上还可以使用图结构或者层次结构设计结构化的注意力分布
- 结构化注意力:略
self-attention v.s. attention ?
下面再介绍一种具体的注意力模型,非常重要!自注意力模型!
自注意力模型也是一种注意力模型,但是需要满足下面几个条件:
- 使用键值对注意力 (KQV 模型)
- K、Q、V 分别使用下式计算
$K=W_KX, Q=W_QX, V=W_VX$, 其中 X 为输入序列,三个 W 为可训练的参数。
需要指出的是:如果使用缩放点积模型 (dot product) 作为打分函数,那么:
$self-att(Q,K,V)=Vsoftmax(\frac{K^TQ}{\sqrt{d_k}})\ where\ K\in\Bbb{R^{d_k\times N}}\ with\ N\ the\ length\ of\ X$
自注意力模型的“自”就表示“由 X 自己的线性组合生成K、Q、V” 自注意力模型可以作为神经网络的一层来使用 网上说,自注意力是 K=Q=V,个人感觉显然不对。
Seq2Seq 模型
序列到序列模型,也就是输入是一个序列,输出是一个序列,例如:机器翻译、问答系统等。
句子的数学表达
首先我们有一个词表文件 V, 用来存储自然语言中的所有词语,所以,|V|非常的大,它是几万甚至几十万。这个词表中的词汇是有顺序编号的,例如:“阿斗”(词表第一个词)编号为1,“做作”(词表最后一个词)编号为664320,那么,“阿斗”的数学表达就是向量$ 1,0,0,…,0$, “做作”的数学表达就是$[0,0,0,…,1]$. 这个向量就叫做词汇的嵌入向量表示(embedding).
广义的 embedding 为能表示一个文本信息的向量或者张量(即文本的表示),例如,经过编码器处理后的信息(如可以在编码器中聚合语法信息等),也可以叫做文本的 embedding,只不过这个表示人类看不懂,只有人工智能可以看懂,也叫高层语义表示。
Seq2Seq 的目标函数
设输入 $x=x_{1:S}$, 输出 $y=y_{1:T}$
$p_\theta$为参数为$\theta$的概率模型,这个概率模型的参数通过数据集的样本统计分析而得(参数估计问题),我们希望数据集样本数据出现的概率尽可能大,因此:
目标函数为:$p_\theta(y_{1:T}|x_{1:S})=\prod_{t=1}^T{p_\theta(y_t|y_{1:(t-1)}, x_{1:S})}$
给定数据集:${(x_{S_n},y_{T_n})}_{n=1}^N$
采用最大对数似然估计:$max_\theta\sum_{n=1}^Nlog\ p_\theta(y_{1:T_n}|x_{1:S_n})$ 估计参数$\theta$
Seq2Seq 的生成
训练完成得到模型参数$\theta$后,如果给定一个输入序列x,根据下式计算输出序列
$\hat{y}=argmax_y{p_\theta(y|x)}$
Seq2Seq 的模型
那么,$p_\theta$是什么呢?它就是一个深度学习模型!
有以下三种:最重要的是基于自注意力的模型。
-
编码器-解码器模型(Encoder-Decoder)
之前介绍循环神经网络 RNN 的时候有介绍过,结构示意图如下:
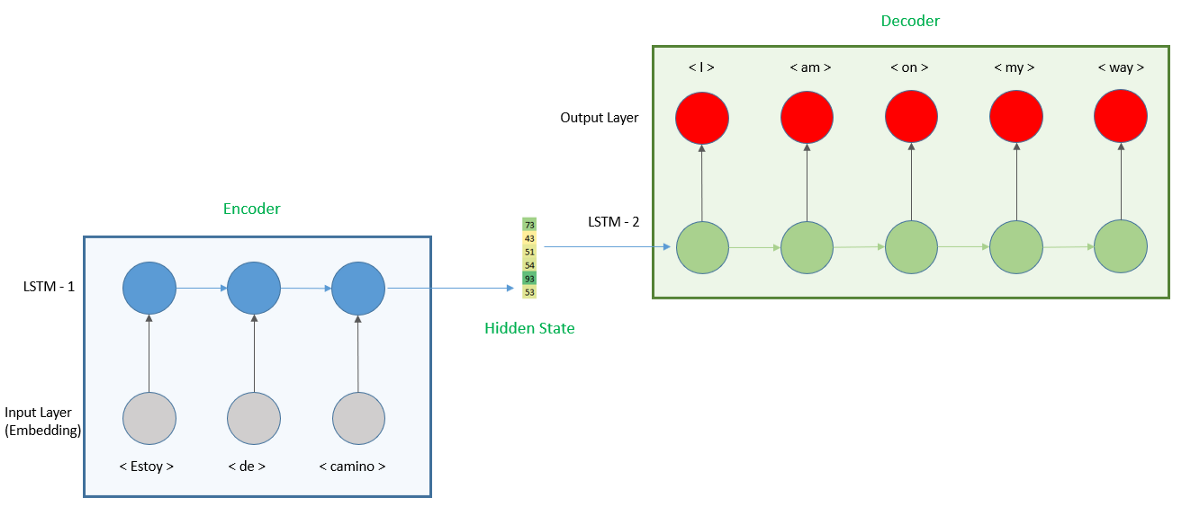
- 基于注意力的模型:在解码过程的第t步时,用上一步t-1的隐状态作为查询向量,从所有输入序列的隐状态中选择相关信息。
- 基于自注意力的模型:Transformer
Transformer
好了,终于到了大名鼎鼎的 Transformer !
自注意力模型
见上面 self-attention v.s. attention ? 部分
这里设输入序列为 H.
多头自注意力
$MultiHead(H)=W_O[head_1;…;head_M]$
$head_m=self-att(Q_m,K_m,V_m)$
$\forall{m\in{1,…,M}}, Q_m =W_Q^mH,K_m =W_K^mH,V_m =W_V^mH,$
也就是说,查询向量有 M 个!
注意和上面第二节的多头注意力进行比对!
位置编码
自注意力模型忽略了输入序列中词汇的位置信息,因此需要加入位置编码来修正。
设输入序列 $H^{(0)}=[e_{x_1}+p_1, …, e_{x_T}+p_T]\ with\ e_{x_t}\ the\ embedding\ vector, p_t\ the\ positional\ encoding$
$p_t$ 可以作为可学习的参数,也可以预定义: $p_{t,2i}=sin(t/10000^{2i/d})$
$p_{t,2i+1}=cos(t/10000^{2i/d})$
表示第t个位置的编码向量的第2i维,d是编码向量的维度
编码器 (Encoder)
第一个运算:层归一化 (layer normalization)
$Z^{(l)}=norm(H^{(l-1)}+MultiHead(H^{(l-1)}))$
第二个运算:逐位置的前馈神经网络
$FNN(z)=W_2ReLu(W_1z+b_1)+b_2$
第三个运算:层归一化
$H^{(l)}=norm(Z^{(l)}+FFN(Z^{(l)}))$
解码器 (Decoder)
第一个模块:Masked Multi-Head Attention
理想状况是,使用自注意力模型对已生成的前缀序列 $y_{1:(t-1)}$进行编码得到 $H^d=[h_1^d,…,h_{(t-1)}^d]$. 但由于在训练时,解码器的输入为整个目标序列,这时可以通过一个掩码(Mask)来选择特定长度的序列。
第二个模块:解码器到编码器注意力模块:使用$h_{(t-1)}^d$作为查询向量,通过注意力机制从输入序列$H^e$中选取有用的信息。
第三个模块:逐位置的前馈神经网络